처음 Lightsail로 이사왔을 때 인스턴스 선택에는 큰 고민을 들이지는 않았다. 제공되는 WordPress instance에는 필요한 것들이 이미 다 설치 되어 있어서 인스턴스를 하나 생성하고 기존 블로그를 import하는 것으로 모든 과정들이 비교적 순조롭게 진행된 편이었다. 문제는 이 WordPress 인스턴스가 Bitnami로 되어 있어서 세부적인 관리 작업에는 제약이 많다는 점이다. 그래서 AWS에 최적화 되어 있다는 Amazon Linux2023(AL2023)으로 LEMP를 직접 설치하고 기존의 블로그를 수동으로 마이그레이션 해 보기로 했다.
이번 포스팅에서는 AL2023 인스턴스에 LEMP(Linux, Nginx, MariaDB, PHP)를 설치하고 Bitnami에서 사용하던 데이터베이스와 자료들을 수동으로 옮겨오는 과정을 설명한다. All-in-One 같은 편리한 마이그레이션 유틸리티를 쓰지 않고 굳이 수작업으로 일일이 옮겨야 했던 이유는 All-in-One에서 띄운 오류 때문이었는데 아무런 문제가 없고, 기술적 호기심 또한 없다면 굳이 이 내용을 따라 수작업으로 옮길 필요는 없을 것이다.
AL2023 환경 구축
Lightsail에서 AL2023 인스턴스를 생성한 뒤 시스템을 업데이트하고 LEMP 패키지를 설치한다. Amazon Linux 2023은 Fedora기반으로 패키지 관리에 dnf 명령어를 사용한다. PHP8.3과 필요한 패키지들을 설치해 주고 나서 Nginx, MariaDB, PHP-FPM 서비스들을 실행해 준다.
sudo dnf update -y sudo dnf install -y nginx mariadb105-server php8.3 php8.3-fpm php8.3-mysqlnd php8.3-gd php8.3-xml php8.3-mbstring php8.3-bcmath php8.3-opcache php8.3-intl php8.3-zip # 서비스 활성화 및 자동 실행 설정 sudo systemctl start nginx mariadb php-fpm sudo systemctl enable nginx mariadb php-fpm
데이터베이스 초기화
MariaDB에 WordPress를 위한 database를 생성하고 비밀번호를 설정한다. mysql_secure_installation은 여러 보안 관련한 처리를 해주는데, 사용하지 않는 기능들을 끄거나 비밀번호를 설정하는 과정을 진행해 준다.
설정이 끝나면 root user로 data base를 실행시킨다.
sudo mysql_secure_installation sudo mysql -u root -p
wordpress database를 생성하고, wpuser사용자를 생성한 다음 권한을 설정하는 과정이다. 나는 비밀번호를 새롭게 만들지 않고 기존에 Bitnami가 생성해 주었던 database 비밀번호(wp-config.php에 있는)를 그대로 사용했다.
CREATE DATABASE wordpress DEFAULT CHARACTER SET utf8mb4 COLLATE utf8mb4_unicode_ci; CREATE USER 'wpuser'@'localhost' IDENTIFIED BY '[사용자_비밀번호]'; GRANT ALL PRIVILEGES ON wordpress.* TO 'wpuser'@'localhost'; FLUSH PRIVILEGES; EXIT;
워드프레스 설치 및 파일 권한 설정
최신 버전의 워드프레스를 다운로드 받아서 /var/www/html/ 위치에 풀어준다.
# 최신 워드프레스 다운로드 wget https://wordpress.org/latest.tar.gz tar -xzf latest.tar.gz sudo cp -r wordpress/* /var/www/html/
AL2023 환경에서 Nginx가 파일을 정상적으로 제어할 수 있도록 소유권과 권한을 수정한다.
# /var/www/html안에 있는 파일들의 권한 설정
sudo chown -R nginx:nginx /var/www/html
sudo find /var/www/html -type d -exec chmod 755 {} \;
sudo find /var/www/html -type f -exec chmod 644 {} \;
# PHP-FPM 실행 그룹을 apache에서 nginx로 변경
sudo sed -i 's/user = apache/user = nginx/g' /etc/php-fpm.d/www.conf
sudo sed -i 's/group = apache/group = nginx/g' /etc/php-fpm.d/www.conf
# 서버 재실행
sudo systemctl restart php-fpm
Nginx 설정
/etc/nginx/conf.d/wordpress.conf 파일을 생성하고 아래의 내용을 추가한다. 이 단계에서 나는 server_name 항목에 “[도메인이름]” 대신에 “_”를 넣어주었고 마이그레이션이 끝나고 나서 기존에 사용하던 public IP를 새로운 인스턴스에 연결시킨 다음에 SSL을 업데이트 하는 과정에서 도메인 이름으로 변경해 주었다.
server {
listen 80;
server_name [도메인이름];
root /var/www/html;
index index.php index.html;
location / {
try_files $uri $uri/ /index.php?$args;
}
location ~ \.php$ {
fastcgi_pass unix:/run/php-fpm/www.sock;
fastcgi_index index.php;
include fastcgi_params;
fastcgi_param SCRIPT_FILENAME $document_root$fastcgi_script_name;
}
}
설정 후 Nginx를 재실행한다.
sudo systemctl restart nginx
여기까지 되었으면 instance의 IP로 접속했을 때 WordPress의 설치 화면이 보이게 된다.
마이그레이션 수작업
먼저 기존 Bitnami 서버 터미널에서 데이터베이스와 콘텐츠를 가져온다.
# 데이터베이스 덤프 mysqldump -u root -p bitnami_wordpress > backup.sql # 데이터 압축 (wp-content와 환경설정파일) cd /opt/bitnami/wordpress tar -czvf wp_data.tar.gz wp-content wp-config.php
추출한 backup.sql과 wp_data.tar.gz 파일을 새 서버로 전송하고, wp_data.tar.gz 파일은 /var/www/html/ 아래에 풀어준다.
# wp-content 복원 tar -xzvf wp_data.tar.gz sudo cp -r wp-content/* /var/www/html/wp-content/
DB Import 및 연결 정보 수정
Database backup file을 import 한다.
# Database back up file import sudo mysql -u root -p wordpress < backup.sql
Database import가 완료되면 /var/www/html/wp-config.php 파일을 열어 새로운 정보로 DB_NAME, DB_USER, DB_PASSWORD를 맞춰준다.
여기까지 해서 모든 이전이 잘 수행 되었다면 기존 인스턴스에서 사용하던 Public IP 주소를 떼어다가(detach) 새로운 인스턴스에 붙여(attach)해 준다. 이 과정은 Lightsail의 “네트워크” 항목에서 진행하면 된다.
많은 가이드 문서에서 마이그레이션 이후 IP정보를 업데이트 하는 과정을 거치는데, Lightsail의 경우는 public IP를 그대로 새로운 instance로 옮겨올 수 있어서 이 부분의 귀찮은 과정을 생략할 수 있다.
새로운 HTTPS 인증서 적용
Public IP가 옮겨지고 domain name으로 접속이 잘 이루어진다면, 앞서 말했던 것 처럼 /etc/nginx/conf.d/wordpress.conf 파일의 server_name 부분에 도메인이름을 적어주고 아래의 과정을 따라서 인증서 정보를 업데이트 해준다.
인증서 업데이트를 위한 Certbot 설치
# Certbot 설치 sudo dnf install -y certbot python3-certbot-nginx # Certbot으로 인증서 업데이트 (Litcoder.com) sudo certbot --nginx -d Litcoder.com -d www.litcoder.com
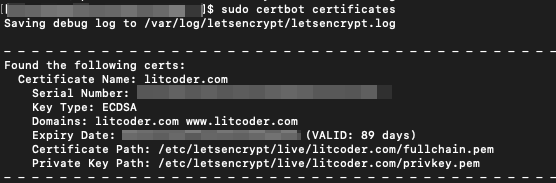
certbot certificates 명령어로 생성된 cert와 유효기간을 확인할 수 있다.
Auto renew service 활성화
Expiration date이 되면 자동으로 인증서를 업데이트 하도록 다음과 같이 certbot-renew.timer 서비스를 활성화 해 준다.
sudo systemctl enable certbot-renew.timer sudo systemctl start certbot-renew.timer
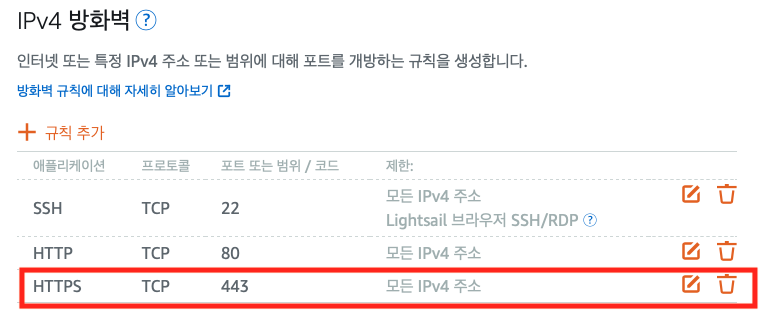
주의! 443은 막혀있다
인증서 업데이트 이후 HTTPS로 접속이 안된다면 443번 포트가 열려 있는지 확인해 보자. Lightsail은 2026년 현재 새롭게 생성한 인스턴스의 22번과 80번 포트만 기본으로 열려 있다. HTTPS를 사용하려면 명시적으로 사용자가 443번을 열어야 한다.
결론
다소 번거로운 과정이기는 했지만, 장기적 관점으로 봤을 때는 Bitnami의 제한에서 벗어나 서버에 대한 세부적인 제어 권한을 가져올 수 있게 되었다는 점에서 시간을 들여 투자해 볼만 한 삽질 이었던 것 같다.